Arrows and Demons

My recent post about randomness and non-randomness spawned a lot of comments over on cosmic variance about the nature of entropy. I thought I’d add a bit about that topic here, mainly because I don’t really agree with most of what is written in textbooks on this subject.

The connection between thermodynamics (which deals with macroscopic quantities) and statistical mechanics (which explains these in terms of microscopic behaviour) is a fascinating but troublesome area.  James Clerk Maxwell (right) did much to establish the microscopic meaning of the first law of thermodynamics he never tried develop the second law from the same standpoint. Those that did were faced with a conundrum.  

 

The behaviour of a system of interacting particles, such as the particles of a gas, can be expressed in terms of a Hamiltonian H which is constructed from the positions and momenta of its constituent particles. The resulting equations of motion are quite complicated because every particle, in principle, interacts with all the others. They do, however, possess an simple yet important property. Everything is reversible, in the sense that the equations of motion remain the same if one changes the direction of time and changes the direction of motion for all the particles. Consequently, one cannot tell whether a movie of atomic motions is being played forwards or backwards.

This means that the Gibbs entropy is actually a constant of the motion: it neither increases nor decreases during Hamiltonian evolution.

But what about the second law of thermodynamics? This tells us that the entropy of a system tends to increase. Our everyday experience tells us this too: we know that physical systems tend to evolve towards states of increased disorder. Heat never passes from a cold body to a hot one. Pour milk into coffee and everything rapidly mixes. How can this directionality in thermodynamics be reconciled with the completely reversible character of microscopic physics?

The answer to this puzzle is surprisingly simple, as long as you use a sensible interpretation of entropy that arises from the idea that its probabilistic nature represents not randomness (whatever that means) but incompleteness of information. I’m talking, of course, about the Bayesian view of probability.

 First you need to recognize that experimental measurements do not involve describing every individual atomic property (the “microstates” of the system), but large-scale average things like pressure and temperature (these are the “macrostates”). Appropriate macroscopic quantities are chosen by us as useful things to use because they allow us to describe the results of experiments and measurements in a  robust and repeatable way. By definition, however, they involve a substantial coarse-graining of our description of the system.

Suppose we perform an idealized experiment that starts from some initial macrostate. In general this will generally be consistent with a number – probably a very large number – of initial microstates. As the experiment continues the system evolves along a Hamiltonian path so that the initial microstate will evolve into a definite final microstate. This is perfectly symmetrical and reversible. But the point is that we can never have enough information to predict exactly where in the final phase space the system will end up because we haven’t specified all the details of which initial microstate we were in.  Determinism does not in itself allow predictability; you need information too.

If we choose macro-variables so that our experiments are reproducible it is inevitable that the set of microstates consistent with the final macrostate will usually be larger than the set of microstates consistent with the initial macrostate, at least  in any realistic system. Our lack of knowledge means that the probability distribution of the final state is smeared out over a larger phase space volume at the end than at the start. The entropy thus increases, not because of anything happening at the microscopic level but because our definition of macrovariables requires it.

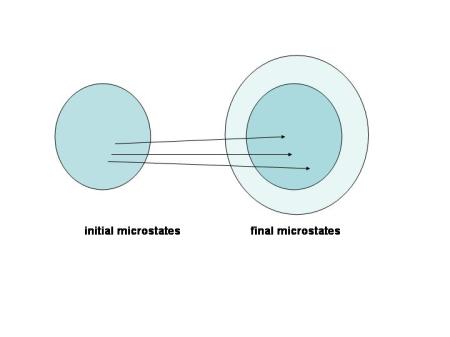
This is illustrated in the Figure. Each individual microstate in the initial collection evolves into one state in the final collection: the narrow arrows represent Hamiltonian evolution.

 

However, given only a finite amount of information about the initial state these trajectories can’t be as well defined as this. This requires the set of final microstates has to acquire a  sort of “buffer zone” around the strictly Hamiltonian core;  this is the only way to ensure that measurements on such systems will be reproducible.

The “theoretical” Gibbs entropy remains exactly constant during this kind of evolution, and it is precisely this property that requires the experimental entropy to increase. There is no microscopic explanation of the second law. It arises from our attempt to shoe-horn microscopic behaviour into framework furnished by macroscopic experiments.

Another, perhaps even more compelling demonstration of the so-called subjective nature of probability (and hence entropy) is furnished by Maxwell’s demon. This little imp first made its appearance in 1867 or thereabouts and subsequently led a very colourful and influential life. The idea is extremely simple: imagine we have a box divided into two partitions, A and B. The wall dividing the two sections contains a tiny door which can be opened and closed by a “demon” – a microscopic being “whose faculties are so sharpened that he can follow every molecule in its course”. The demon wishes to play havoc with the second law of thermodynamics so he looks out for particularly fast moving molecules in partition A and opens the door to allow them (and only them) to pass into partition B. He does the opposite thing with partition B, looking out for particularly sluggish molecules and opening the door to let them into partition A when they approach.

The net result of the demon’s work is that the fast-moving particles from A are preferentially moved into B and the slower particles from B are gradually moved into A. The net result is that the average kinetic energy of A molecules steadily decreases while that of B molecules increases. In effect, heat is transferred from a cold body to a hot body, something that is forbidden by the second law.

All this talk of demons probably makes this sound rather frivolous, but it is a serious paradox that puzzled many great minds. Until it was resolved in 1929 by Leo Szilard. He showed that the second law of thermodynamics would not actually be violated if entropy of the entire system (i.e. box + demon) increased by an amount every time the demon measured the speed of a molecule so he could decide whether to let it out from one side of the box into the other. This amount of entropy is precisely enough to balance the apparent decrease in entropy caused by the gradual migration of fast molecules from A into B. This illustrates very clearly that there is a real connection between the demon’s state of knowledge and the physical entropy of the system.

By now it should be clear why there is some sense of the word subjective that does apply to entropy. It is not subjective in the sense that anyone can choose entropy to mean whatever they like, but it is subjective in the sense that it is something to do with the way we manage our knowledge about nature rather than about nature itself. I know from experience, however, that many physicists feel very uncomfortable about the idea that entropy might be subjective even in this sense.

On the other hand, I feel completely comfortable about the notion:. I even think it’s obvious. To see why, consider the example I gave above about pouring milk into coffee. We are all used to the idea that the nice swirly pattern you get when you first pour the milk in is a state of relatively low entropy. The parts of the phase space of the coffee + milk system that contain such nice separations of black and white are few and far between. It’s much more likely that the system will end up as a “mixed” state. But then how well mixed the coffee is depends on your ability to resolve the size of the milk droplets. An observer with good eyesight would see less mixing than one with poor eyesight. And an observer who couldn’t perceive the difference between milk and coffee would see perfect mixing. In this case entropy, like beauty, is definitely in the eye of the beholder.

The refusal of many physicists to accept the subjective nature of entropy arises, as do so many misconceptions in physics, from the wrong view of probability.